Wiskunde 1ste graad A
Ruimtemeetkunde 1ste graad A
In de wiskunde heb je naast vlakke meetkunde ook ruimtemeetkunde. Welke ruimtefiguren bestaan er, hoe zit het met de onderlinge ligging van rechten, hoe teken je zo'n ruimtefiguur op een blad? Bart legt het je allemaal uit!
Ruimtemeetkunde
De meetkunde in de wiskunde kan je eigenlijk onderverdelen in twee grote stukken: de vlakke meetkunde en de ruimtemeetkunde. In dit hoofdstuk kom je alles te weten over ruimtemeetkunde. Misschien denk je bij het woord ‘ruimte’ meteen aan space shuttles, ruimtereizen naar Mars of het internationale ruimtestation ISS. In de wiskunde betekent het begrip ‘ruimte’ echter iets anders. Het is eigenlijk alles wat er rond ons is en waarin we ons kunnen bewegen.
Het verband tussen ruimtefiguren en veelvlakken
De meeste voorwerpen die we kennen zijn ruimtefiguren, in de wiskunde ook wel lichamen genoemd. Het zijn voorwerpen die een plaats innemen in de ruimte. Een veelvlak is ook een ruimtefiguur, maar dan wel een speciale. Een veelvlak is namelijk een ruimtefiguur met alleen maar veelhoeken als grensvlakken. De bekendste en belangrijkste voorbeelden van een veelvlak is een balk of een kubus.
Ruimtefiguren herkennen
Hoe kan je ruimtefiguren herkennen? Dat is een interessant vraag die Bart graag voor je beantwoordt. Je zal zien dat elk vlak van een kubus een vierkant is en dat een balk enkel rechthoeken heeft als zijvlakken. Een cilinder heeft als grondvlak en bovenvlak een cirkel die verbonden zijn door rechte lijnen die samen een mantel vormen. Een recht prisma lijkt op een cilinder, maar dan wel met een veelhoek als grondvlak en bovenvlak. Een piramide in de wiskunde is dan weer te herkennen omdat het grondvlak een veelhoek is waarvan alle hoeken verbonden zijn aan eenzelfde punt dat erboven ligt. Een kegel lijkt op een piramide, met het grote verschil dat het grondvlak geen veelhoek, maar een cirkel is. Een bol, denk bijvoorbeeld aan onze wereldbol, of een voetbal, is een ruimtefiguur die aan alle kanten rond is. Vind je deze uitleg moeilijk om volgen? Geen probleem, Bart toont het je allemaal in een duidelijke lesvideo.
Oppervlakte kubus, balk en cilinder
Als je de verschillende ruimtefiguren kent, kan je er verder mee aan de slag. Je kan de oppervlakte van een kubus of de oppervlakte van een balk gemakkelijk berekenen door de oppervlakte van alle zijvlakken bij elkaar op te tellen. In plaats van de oppervlakte van elk zijvlak apart te berekenen en dan alles op te tellen, kan je gebruik maken van een simpele formule. Ook voor het berekenen van de oppervlakte van een cilinder bestaat er een eenvoudige formule. Bart laat je zien hoe je dit precies moet doen.
Volume kubus, balk en cilinder
Wat is het volume van een ruimtefiguur? Eigenlijk betekent het volume gewoon de inhoud. Hoe bereken je dit dan precies? Eigenlijk is het spotgemakkelijk: je vermenigvuldigt gewoon de oppervlakte van het grondvlak met de hoogte van de ruimtefiguur. Zowel voor een kubus, een balk als een cilinder kan je dit echter gemakkelijker doen door de juiste formule toe te passen. Bart vertelt je hoe het werkt.
Cavalière perspectief
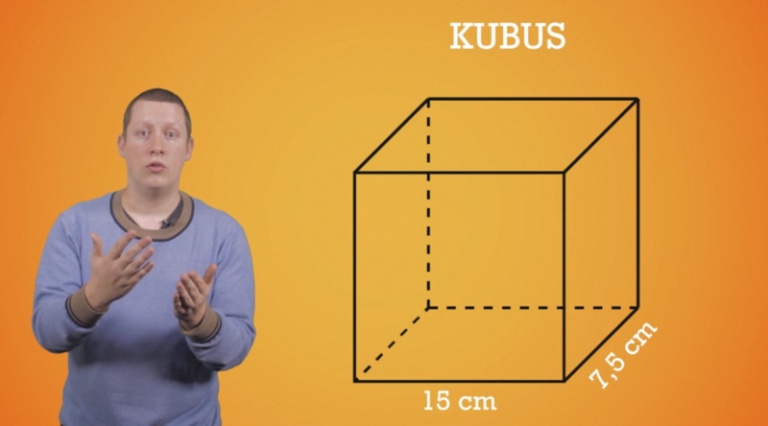
Het Cavalière perspectief…klinkt moeilijk vind je niet? En toch kan het jou net helpen om een kubus en een balk gemakkelijk en foutloos in perspectief te tekenen. De methode bestaat uit een aantal simpele stapjes:
- Teken het voorvlak op ware grootte.
- Evenwijdige rechten, teken je ook evenwijdig.
- Teken de diepte maar half zo lang als ze in werkelijkheid is. En teken de diepte in een hoek van 45°.
OK, we geven het toe, op papier klinkt het nog altijd niet heel duidelijk. Gelukkig hebben we ook een coole lesvideo waarin Bart het je allemaal laat zien.